La notion d’écart est bien connue de la plupart des joueurs. Ceux qui découvrent le mot ont certainement déjà eu l’intuition de ce qu’il recouvre au long de leurs expériences de jeu. Au travers de cette série d'articles, nous allons tacher d'expliquer ce qui se cache derrière cette notion. Dans ce premier article, nous allons, avec quelques exemples simples, définir ce qu'est l'écart. Pour ceux pour qui cette notion est déjà familière, nous vous conseillons de passer directement à la deuxième partie de notre article, consacrée à l'application de la notion d'écart à une méthode de pronostic hippique.
Qu'est que l'écart ?
Au turf, il s’agit du nombre de paris perdus d’affilé avant la réapparition d’un coup gagnant.
Très vite, pour certains, ce terme d’écart pourra avoir pour synonyme poisse, scoumoune, etc.
D’autres, plus rationnels, y verront une manifestation ordinaire de la fameuse loi des séries.
Nous allons voir que le sujet se doit effectivement d’être traité avec beaucoup de rigueur mais qu’il ne nous emmènera pas moins dans des territoires passionnants.
Quelques exemples pour comprendre l'écart
Commençons par une anecdote personnelle qui s’est produite récemment : au cours d’une soirée entre amis, je m’étais fait apostropher sur cette notion de loi des séries. Quelques convives y allaient de leur interprétation ésotérique (mauvais œil et autres chats noirs etc.). Me sachant versé en mathématique, on me demanda de trancher la question.
Opération délicate en peu de temps face à un auditoire qui avait goûté quelques bons vins et un peu en froid avec la chose scientifique pour la majorité. Il me fallait proposer du concret.
Je pris l’exemple suivant pour tenter d’expliquer pourquoi certains événements avaient la fâcheuse tendance à se répéter à outrance (aussi parfois une tendance plus heureuse mais qu’on remarque moins car c’est dans la nature humaine, lié probablement à l’instinct de survie d’être marqué plus en profondeur par le négatif).
Je proposai donc à l’assemblée ceci :
« on demanderait à un garagiste d’effectuer un petit sondage qui consisterait à noter la fréquence à laquelle un même client lui ramène un pneu crevé à réparer (on considérera que le risque de crevaison est le même pour tous, qu’il est complètement aléatoire et que l’on pourra étendre le sondage à tous les garagistes de France et de Navarre pour mieux asseoir notre base statistique).
Quelle serait alors la réponse la plus nombreuse ?
Par exemple l’un des clients dira qu’il n’a pas subi de crevaison depuis 20 ans, un autre que c‘est incroyable mais qu’il a déjà crevé la semaine précédente etc. On ferait alors une croix dans la colonne correspondant à la date et on repérerait ainsi la colonne la plus remplie, c’est à dire l’écart le plus fréquent entre deux crevaisons.»
Autour de la table on argumenta que, de nos jours, on ne crevait plus très souvent et un consensus se fit pour me répondre sans conviction : en moyenne environ tous les 5 ans. Je me fis confirmer que la réponse la plus nombreuse serait j’ai crevé la dernière fois il y a 5 ans et que ce pic des réponses coïncidait donc avec le temps moyen entre 2 crevaisons. De toutes façons, peu importe que ce chiffre corresponde ou non à la réalité de terrain car cela n’enlève rien au processus en jeu.
J’annonçai que la réponse la plus représentée serait : j’ai déjà crevé hier !
Je vis tous les sourcils se froncer et compris qu’il me fallait trouver une explication imparable.
Je pris alors le cas basique du tirage à pile ou face.

Tout le monde accepta que la sortie moyenne de pile par exemple était de 1 fois sur 2 mais que des séquences plus ou moins longues de face s’intercalaient entre 2 apparitions de pile et que ce dernier pour retrouver son incontournable moyenne devait lui aussi à son tour effectuer de longues séries.
Or la longueur d’une série de face étant par principe sans limite, il faut que pile se précipite en écart plus petits que la moyenne pour compenser efficacement (soit des écarts 0 et 1). Après la série de tirage F F F F F F il faut en théorie P P P P P P pour ré obtenir la moyenne : donc 6 écart 0 pour compenser un écart 6.
En poussant le raisonnement à l’extrême (méthode mathématique de la descente infinie) il s’avère donc que l’écart 0 sera le plus fréquent suivi de l’écart 1, du 2 etc.
Vous vous convaincrez aisément de la chose en tenant le compte des écarts des tirages d’un numéro au dé ou à la roulette car même avec une sortie en moyenne tous les 6 jets au dé et tous les 37 tirages à la roulette, la répétition (l’écart 0) sera l’écart le plus fréquent.
Peu à peu, vous vous surprendrez à observer ce phénomène dans des domaines très différents de la vie de tous les jours. Il serait d’ailleurs amusant de tenir à jour une petite collection de la répétition qu’on pensait improbable de phénomènes incongrus comme de voir le même jour deux passants se cogner contre un lampadaire etc.
Afin d’assurer la moyenne, les écarts à gauche de celle-ci (mais limités par 0) doivent être aussi nombreux que ceux à droite de cette même moyenne (mais non limités eux).
La répétition est bien l’événement temporel le plus fréquent !
Voilà la loi des séries, sinon démontrée, du moins mieux saisie.
Pour en finir avec mon anecdote, une amie présente ce soir-là m’appela quelques jours plus tard. « Devine quoi ! j’étais un peu larguée et dubitative l’autre soir avec ton histoire de pneus. Et bien moi qui n’avais jamais crevé depuis des années et des années que je conduis, cela vient de m’arriver deux fois dans la semaine. Je crois que je te dois symboliquement un petit restaurant pour avoir un peu douté de ton explication. » Je n’en demandais pas tant mais me retrouvais bien content que les faits aient corroborés un aspect scientifique un peu abstrait.
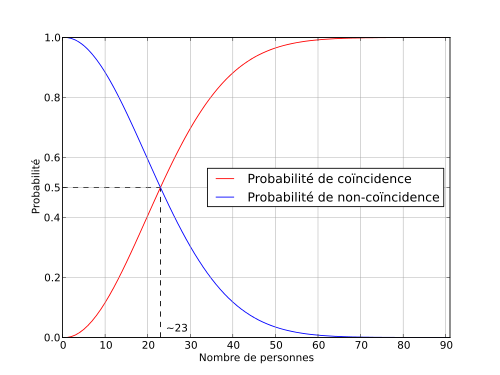
Sur ce thème de notre cerveau nous trompe il existe nombre d’exemples encore plus étonnants que je vous invite à découvrir dans des revues ou sur des sites de mathématiques récréatives, comme le Paradoxe des anniversaires qui prouve sans trop de complication que, dans un groupe de 23 personnes, il y a 1 chance sur 2 que deux d’entre elles soient nées le même jour de l’année, et qu’avec 57 personnes présentes cette probabilité dépasse 99 %, allant ainsi largement à l’encontre de ce que notre esprit nous suggère en première réflexion.
Écart et permanence
On appelle permanence le relevé d’une série de coups gagnants et perdants dans l’ordre chronologique de leur apparition. Pour être significative cette permanence devra être la plus longue possible. Certaines formules de probabilité se contentent d’un échantillon de 30 pour établir des tendances mais plusieurs centaines de coups sont généralement nécessaires avant de tirer des conclusions fiables. Personnellement, je n’effectue aucune analyse avant d’avoir atteint un échantillon de 1 000 coups. Sachant que, même au-delà, des variations parfois invisibles dans les conditions du jeu ou dans notre choix peuvent engager une dérive des chiffres. Il s’avère donc nécessaire de réévaluer régulièrement l’ensemble de la permanence ainsi que la séquence des 1 000 derniers coups pour mettre en évidence une éventuelle évolution de la sélection. Nous verrons une autre fois que cette surveillance permet de coller au plus près du monde des courses qui, comme tous les univers complexes, présente des évolutions et des cycles.
L'écart et les méthodes de turf
Maintenant que la notion d'écart vous parait moins abstraite, je vous conseille de consulter la deuxième partie de cet article consacrée plus précisément à notre passion commune, le turf. En effet, connaître l'écart d'une méthode permet de relativiser une série d'échecs, ou au contraire de réagir pour modifier la méthode en cas de perte de rentabilité.


